내가 보려고 쓴 정리 요약.
알고리즘 분석
정확성을 분석하는 것, 효율성을 분석하는 것. 2가지로 나뉨
정확성 분석
: 유효한 입력에 대해 유한 시간 내에 정확한 결과의 생성 여부
수학적 기법을 사용한 이론적인 증명 과정
(우리가 원하는 결과를 내지 못하면 알고리즘으로써 의미가 없음)
효율성 분석
:알고리즘 수행에 필요한 컴퓨터 자원의 양을 측정/평가
얼마나 많은 메모리를 필요로 하는가.
- 공간 복잡도 (space complexity)
메모리 양 = 정적 공간 + 동적 공간
- 시간 복잡도 (time complexity)
수행시간 = 알고리즘의 실행에서부터 완료까지 걸리는 시간
시간 복잡도
컴퓨터에서 실행시켜 실제 수행시간을 측정하는 방법?
- 실행 환경에 종속적이므로 일반성이 결여된 방법
- 컴퓨터 속도, 구현에 사용된 프로그래밍 언어, 프로그램 작성 방법, 컴파일러의 효율성 등에 따라 시간이 달라짐
알고리즘 수행시간 = ∑{각 문장(연산)이 수행되는 횟수}
수행시간에 영향을 미치는 요인
1. 입력 크기
”입력되는 데이터의 크기”, “문제가 해결하려는 대상이 되는 개체의 개수”
(예: 리스트 원소의 개수, 행렬의 크기, 그래프의 정점의 수 등)
입력 크기 n이 커질수록 수행시간도 증가함.
단순히 단위 연산이 수행되는 개수의 합으로 표현하는 것은 부적절.
-> 위 이유로 입력크기 n의 함수 f(n)으로 표현하게 됨.
2. 입력 데이터 상태
입력 데이터의 상태에 따라 시간이 달라짐.
어떤 입력이 주어졌을게 그것을 수행하는 데 걸리는 시간 -
Sn: 크기 n인 입력들의 집합
P(I): 입력 I가 발생할 확률
t(I): 입력 I일 때 알고리즘의 수행시간

평균 수행시간 : 입력과 걸리는 시간을 계산해서 평균을 냄. 입력이 주어지는 모든 것을 고려한다음에 평균을 내는 것. (이론 적으로는 맞지만, 실질적이지 않음, 시간들을 일일히 다 계산하기 힘듦. 현실적이지 않음.)
최선 수행시간 : 모든 입력된 데이터가 몇가지인지 모르지만 가장 짧게 걸리는 것을 알고리즘의 수행시간이라고 판단함.
최악 수행시간 : 모든 입력된 데이터 중에서 가장 오래걸리는 것을 알고리즘의 수행시간이라고 판단함.
알고리즘의 시간 복잡도는 최악의 수행시간으로 표현한다.
입력크기 n에 대한 함수와 최악의 수행시간으로 표현하다.
근데 왜 최악으로 계산할까?
A,B 두개의 알고리즘 중에서 우열을 가리고 싶음.
A = 최선 3초 , B = 최선 1초. ==> 알수 없음.
A = 최대 3초, B = 최대 5초. ==> 아, 그래도 A가 빠르겠구나 짐장할 수 있음.
최선의 경우
집 -보도 - 버스 - 자하철 - 보도 - 회사 = 60분
최악의 경우
집 -보도 - 버스 - 자하철 - 보도 - 회사 = 89분
평균의 경우
집 -보도 - 버스 - 자하철 - 보도 - 회사 = 75분
지각하지 않게 가려면 몇 분을 잡고 가야할 까? -> 안전하게 간다면 89분을 기준으로 집에서 나와야함. (시간안에는 해결)
SumAverage(A[], n) //n은 입력크기 // A[0..n-1], n : 입력 배열과 데이터 갯수.
{
sum = 0; //count: 1
i = 0; //count: 1
while ( i < n ) { //count: n+1
sum = sum + A[i]; //count: n
i = i + 1; //count: n
}
average = sum / n; //count: 1
print sum, average; //count: 1
}
각각의 문장들이 실행되는 횟수를 다 더함.
알고리즘 수행시간 T(n) = 3n + 5
만약, 내가 처리해야할 데이터가 10개면? 35번 수행, 1000개면? 3005번 수행.
알고리즘 수행시간 T(n) = 3n + 5 ===> 점근성능 빅오(Big-oh)표기법. ==> O(n)
수행시간을 표기하고 싶어! 빅오 표기법으로 표현 -> 이것을 점근성능이라고함.
점근성능
점차적으로 가까이 가는 성능.
입력 크기 n이 무한히 커짐에 따라 결정되는 성능.

이 둘중에 어떤 게 더 성능이 좋을까?
n = 5 일 때,
첫번째는 59, 두번째는 27.5
숫자가 적은게 수행되는 횟수가 적으니까 당연히 27.5가 더 좋은거임.
그러나
n = 10일 때, 첫번째는 109, 두번째는 80
n = 15일 때, 첫번째는 159, 두번째는 157.5
n = 16일 때, 첫번째는 169, 두번째는 176
n = 20일 때, 첫번째는 209, 두번째는 260
...
16일때와 20일때는 첫번째가 더 성능이 좋음.
그래서, 증가하는 추세, 어떤 식으로 무한히 커질거냐 ? 가 중요함. 아래를 보면.
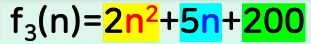
3개의 항으로 이루어진 다항식에서 A(노랑),B(파랑),C(녹색) 값 중 무엇이 가장 영향이 클까?를 따졌을 때.
n = 1, 2+5+200 = 207
n = 5, 50 + 25 + 200 = 275
n = 10, 200 + 50 + 200 = 450
n = 20, 800 + 100 + 200 = 1,100
...
n = 1000, 2,000,000 + 5,000 = 2,005,200
알게된 사실,
n 이 커지면 커질 수록 함수값도 커진다. 커지는 것에 가장 영향을 크게주는 것은? ==> A
점근성능의 결정 방법
입력크기가 충분히 커짐에 따라 함숫값에 가장 큰 영향을 미치는 차수를 찾음.
수행시간의 다항식 함수에서 최고차항만을 계수 없이 취해서 표현. ===> n2을 찾았듯이.
최고차항이 뭔가? 만 찾아내면 됨.
그러나, n과 n2은 수행시간의 정확한 값이 아닌 어림 값일 뿐이다. 그럼에도 사용한는 이유는
- 수행시간의 증가 추세를 파악하는 것이 쉬움.
- 알고리즘 간의 우열을 따질 때 유용. 알고리즘간의 우열 표현/비교에 용이.
점근성능의 표기법
정의1
- 'Big oh' 점근적 상한
함수 f와 g를 각각 양의 정수를 갖는 함수라 하자.
어떤 양의 상수 c 와 n₀이 존재하여
모든 n² ≥ n₀ (모든 경우)에 대하여 f(n) ≤ c·g(n) (작거나 같으면)(부등호를 통해 항상 그래프 상은 아래에 있다는 걸 알 수 있음)이면, f(n) = O(g(n))이다.
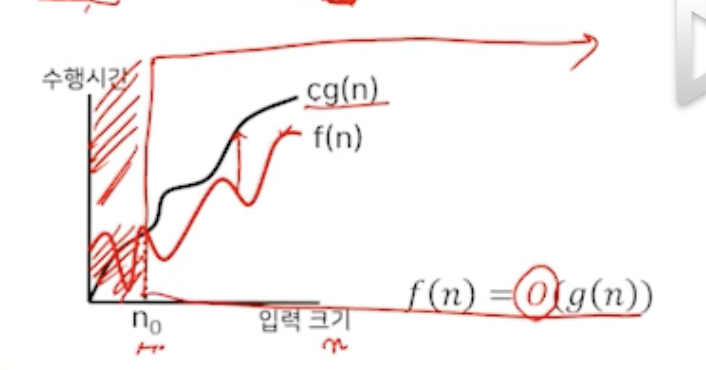
f(n)이 cg(n)이라는 함수보다 작거나 같음.
그래서 f(n)이 아무리 커져도 cg(n)보다 더 이상 커질 수 없음 ==> 점근적인 상한(위에 있는 한계)
이걸 빅오표기로 해서 나타내겠다는 의미.
"최악"의 수행시간을 나타냄.
아무리 나빠도 cg(n)보다 나빠질 수 없다는 뜻.
정의2
- 'Big omega' 점근적 하한
함수 f와 g를 각가각 양의 정수를 갖는 함수라 하자.
어떤 양의 상수 c 와 n₀이 존재하여
모든 n² ≥ n₀ (모든 경우)에 대하여 f(n) ≥ c·g(n) (크거나 같으면)이면, f(n) = Ω(g(n))이다.
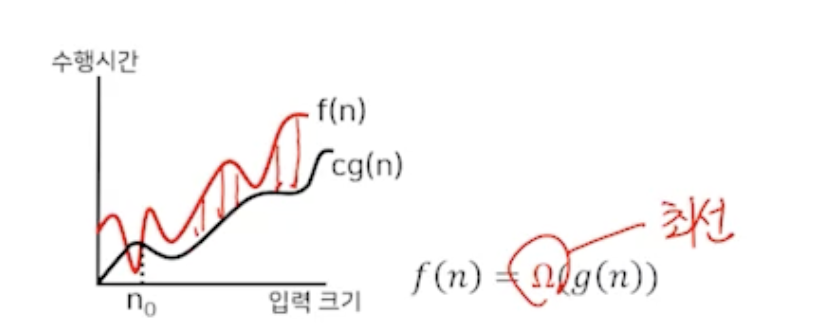
f(n)이 항상 cg보다 우위에 있음.
바꿔 말하면, f(n)이 아무리 낮아져도 아무리 알고리즘 수행시간이 좋아도 cg보다 더 낮아 질 수 없다는 뜻.
"최선"의 수행시간을 나타냄
아무리 좋아도 cg(n)보다 좋아질 수 없음.
정의3
- 'Big theta' 점근적 상하한
함수 f와 g를 각가각 양의 정수를 갖는 함수라 하자.
어떤 양의 상수 c₁ , c₂ 와 n₀이 존재하여
모든 n² ≥ n₀ (모든 경우)에 대하여 c₁ ·g(n) ≤ f(n) ≤ c₂ ·g(n) 이면, f(n) = Θ(g(n))이다.
ㄴ Ω ㄴ O
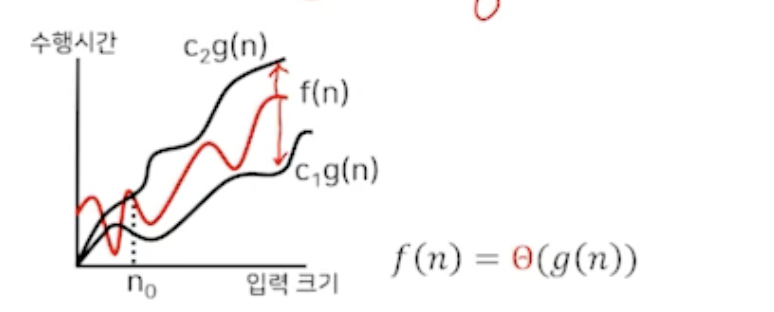
f(n)이 항상 어느 범위에 딱! 있는 것.
빅 세타는 최선의 수행시간과 최악의 수행시간이 같은 범위의 경우.
아무리 좋아도 아무리 나빠도 딱 요정도다.
정리하자면, 함수 f(n)과 g(n)이 있는데, 빅 오던 빅 오메가던 빅 세타가 되기 위해서는 상수 c 와 어떤 n을 찾아가지구
위 식과 같은 관계를 만들 수 있느냐를 따지게 되는 것.
예시로
f(n) = 3n+3, g(n) = n
c = 5, n₀ = 2이 존재하여, n ≥ 2인 모든 n에 대해서
f(n) ≤ c·g(n), 즉 3n + 3 ≤ 5·n을 만족(참) ==> f(n) = O(g(n)) = O(n) 표기
- Big-O를 증명하려면 f(n) ≤ c⋅g(n)을 만족하는 c와 n₀를 찾아야 함.
- 3n + 3 ≤ 5n 을 만족하는지 확인 → n ≥ 3/2.
- n₀ = 2에서 항상 성립하므로, O(n) 표기가 가능함.
(play_ 30:00)
[추가 예시]

n에는 최고차항만 넣으면 됨.
이것만 기억해. f(n)이 주어졌을 때 f(n)에 최고차항을 그대로 쓰면된다. (n)자리에.
주요 O-표기 간 연산 시간의 크기 관계
어떤 하나의 문제에 대해서 알고리즘이 3개가 있었다. 이 알고리즘의 수행시간을 계산 했더니 아래와 같다.
그러면 이 알고리즘의 성능을 빅 오 표기법으로 나타내면? 빅오는 "최악"의 시간
f₁(n) = 10n + 9 f₂(n) = n²/2+3 f₃(n) = 3n³+3n+2
ㄴ O(n) ㄴ O(n²) ㄴ O(n³)
그래서, 3개의 알고리즘 중에서 어떤게 성능이 좋을까?
들어가는 최고차항을 대입.
제곱이니까 예를들면 첫번째 순으로 10, 100, 1000 이 될 수 있음.
그래서 첫번째가 가장 성능이 좋음.

왼쪽에서 오른쪽으로 갈수록 시간이 오래 걸리기 때문에, 효율성이 떨어짐.
O(1)은 상수시간이라 고정이라고 보면됨. 늘어나지 않기 때문에 제일 적다.
[빅오 함수에 따른 연산 시간의 증가 추세]
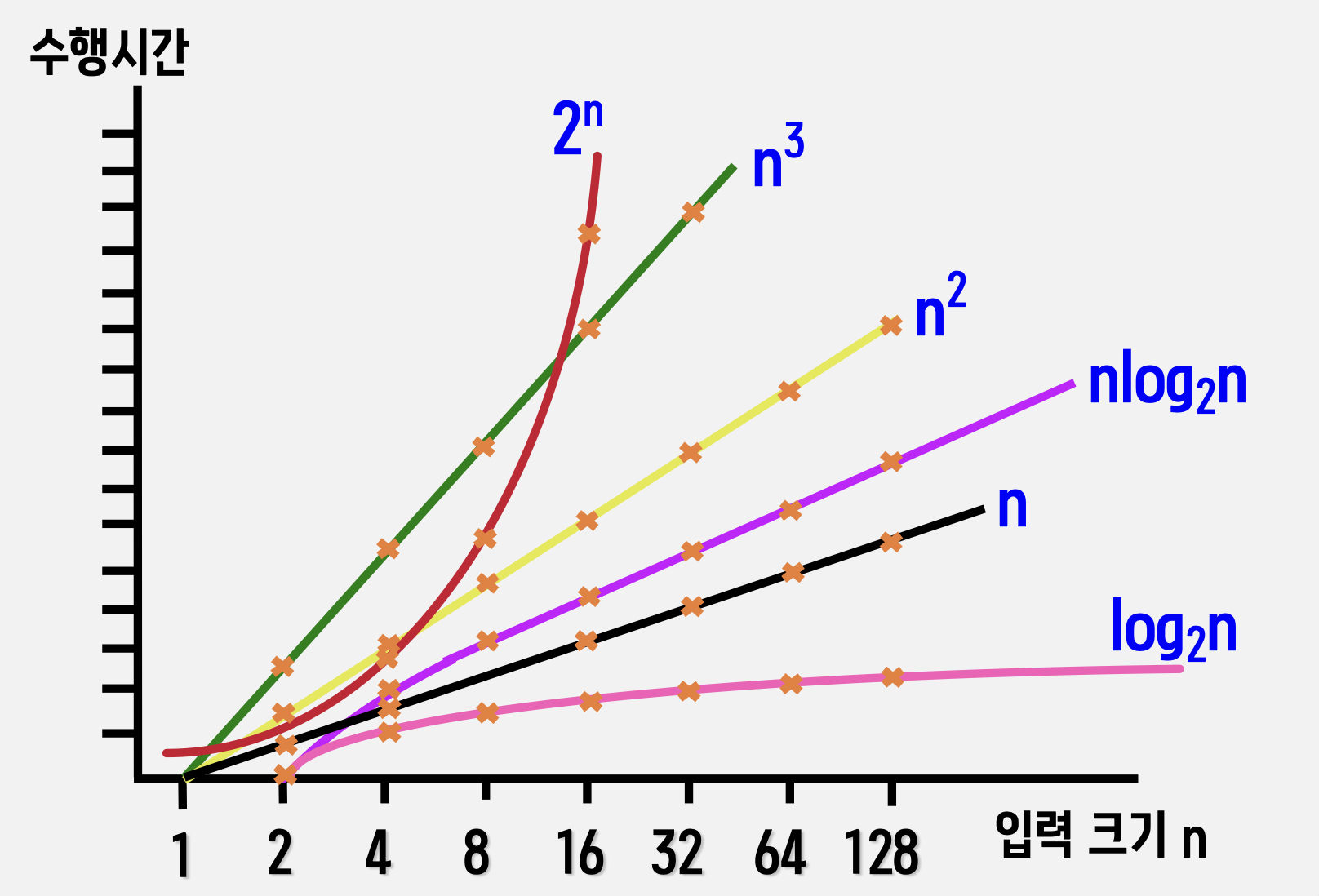
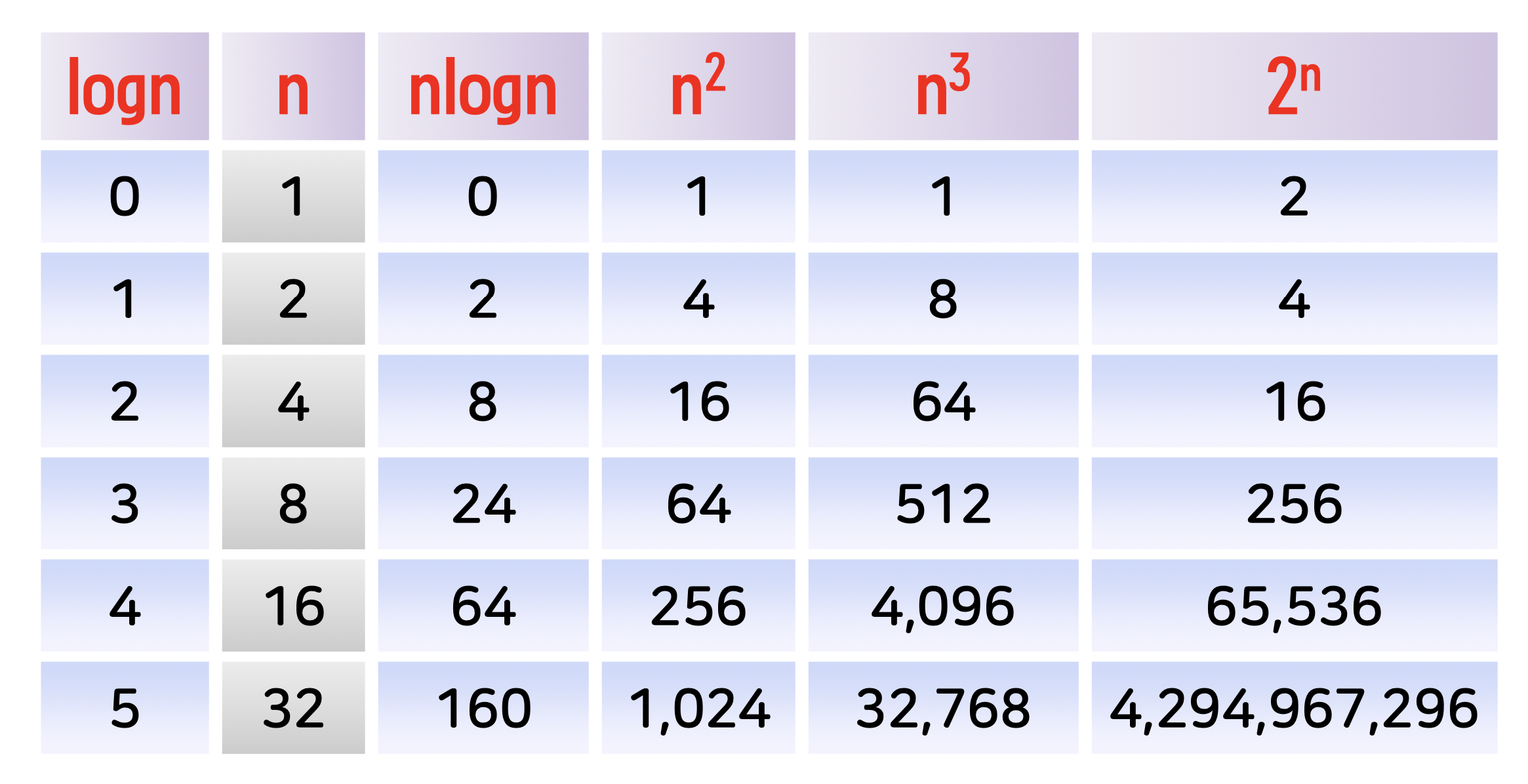
알고리즘의 시간 복잡도 구하기
알고리즘의 시간 복잡도를 구하려면
기본 연산의 수행 횟수의 합 f(n)을 구한 후,
f(n)=O(g(n))을 만족하는 최소 차수의 함수 g(n)을 찾음.
우리가 실제로 사용하는 것은 점근성능이기때문에 이렇게 하지 않아도됨.
실용적인 접근 방법은
알고리즘의 모든 문장이 아닌 루프의 반복 횟수만을 조사하여
최고 차수를 시간 복잡도로 취함.
===> O(최고차수)
예를 들어서,
i = 1; //1 => 계산(x)
while (i <= n) { //n+1 => 계산(o)
x = x + 1; //n => 계산(x)
i = i + 1; //n => 계산(x)
}
ㄴ f(n) = 3n+2 => O(n)
일때,
만약, 상수가 500개, n이 200번이면,
200n + 501 이 될텐데, 이렇게 할 필요 없이
숫자 다 떼고 n만 보면 된다는 뜻임. while 내부는 알고리즘 수행시간을 계산하는데 영향을 끼치지 않음, 상수 부분도 알고리즘 수행시간을 계산하는데 영향을 끼치지 않음. 남는 곳은 반복문. 아, n과 선형적인 구조를 가지고 있구나해서, O(n)으로 판단.
두번째 예로 들어서,
count = 0; //1
for (i=0; i<n; i++) //n+1 => 계산(o)
for (j=0; j<n; j++) //n+1 => 계산(o)
count ++; //1
print count; //1
ㄴ f(n) = n²+2n+4 => O(n²)
반복문 2개니까 제곱.
순환 알고리즘
: recursion, 재귀 알고리즘
알고리즘의 수행 과정에서 자기 자신의 알고리즘을 다시 수행하는 형태 .
이진탐색때 사용. 절반을 나누고 탐색하는 함수를 값을 찾을 때까지 순환.
대체로 점화식으로 표현. 어떤 하나의 값이 자기 자신을 표현하는 수식으로 표현하는 식.
T(n) = T(n/2) + O(1), T(1) = c₁
이진 탐색 수행시간을 T(n)이라고 했을때, 총 걸리는 시간.
(play_ 45:00)

점화식의 폐쇄형

이 점화식의 폐쇄형은 이거고, Θ(log₂n)
이진탐색의 성능은 ? = 빅 세타 Θ(log₂n)다. 라고 말할 수 있음.
기본 점화식과 폐쇄형 6가지

(1),(2)와 (3),(4)와 (5),(6)끼리 비슷
(1) 데이터 n개를 처리하는데 걸리는 시간은, n-1개를 순환호출하고 걸리는 시간에다가 상수시간만큼만 더 걸리느냐,
(2) 데이터 n개를 처리하는데 걸리는 시간은, n-1개를 순환호출하고 걸리는 시간에다가 데이터 갯수에 비례하는 시간만큼 더 걸리느냐
(3) 데이터 n개를 처리하는데 걸리는 시간은, 데이터 2분의 n개를 처리하는 시간에다가 상수시간 만큼 더 걸리느냐,
(4) 데이터 n개를 처리하는데 걸리는 시간은, 데이터 2분의 n개를 처리하는 시간에다가 데이터 갯수에 비례하는 시간만큼 더 걸리느냐
(5) 데이터 n개를 처리하는데 걸리는 시간은, 반반씩 나눴을때 2분의 n, 2분의 n 두개를 나눈 시간에다가, 상수시간 만큼 더 걸리느냐,
(5) 데이터 n개를 처리하는데 걸리는 시간은, 반반씩 나눴을때 2분의 n, 2분의 n 두개를 나눈 시간에다가, 데이터 갯수에 비례하는 시간만큼 더 걸리느냐.
(1) T(n) = Θ(n)
(2) T(n) = Θ(n²)
(3) T(n) = Θ(logn)
(4) T(n) = Θ(n)
(5) T(n) = Θ(n)
(6) T(n) = Θ(nlogn)
이 6개 중에서 다 외우면 좋겠지만 못 외우겠다, 하면 (2),(3),(6)은 반드시 외워야한다.
퀵 정렬("최악의 경우") Θ(n²),
이진 탐색 Θ(logn),
합병 정렬, 퀵정렬("최선의 경우") Θ(nlogn)을 제외한 나머지는 모두 Θ(n)이니까~.
효율적인 알고리즘의 중요성
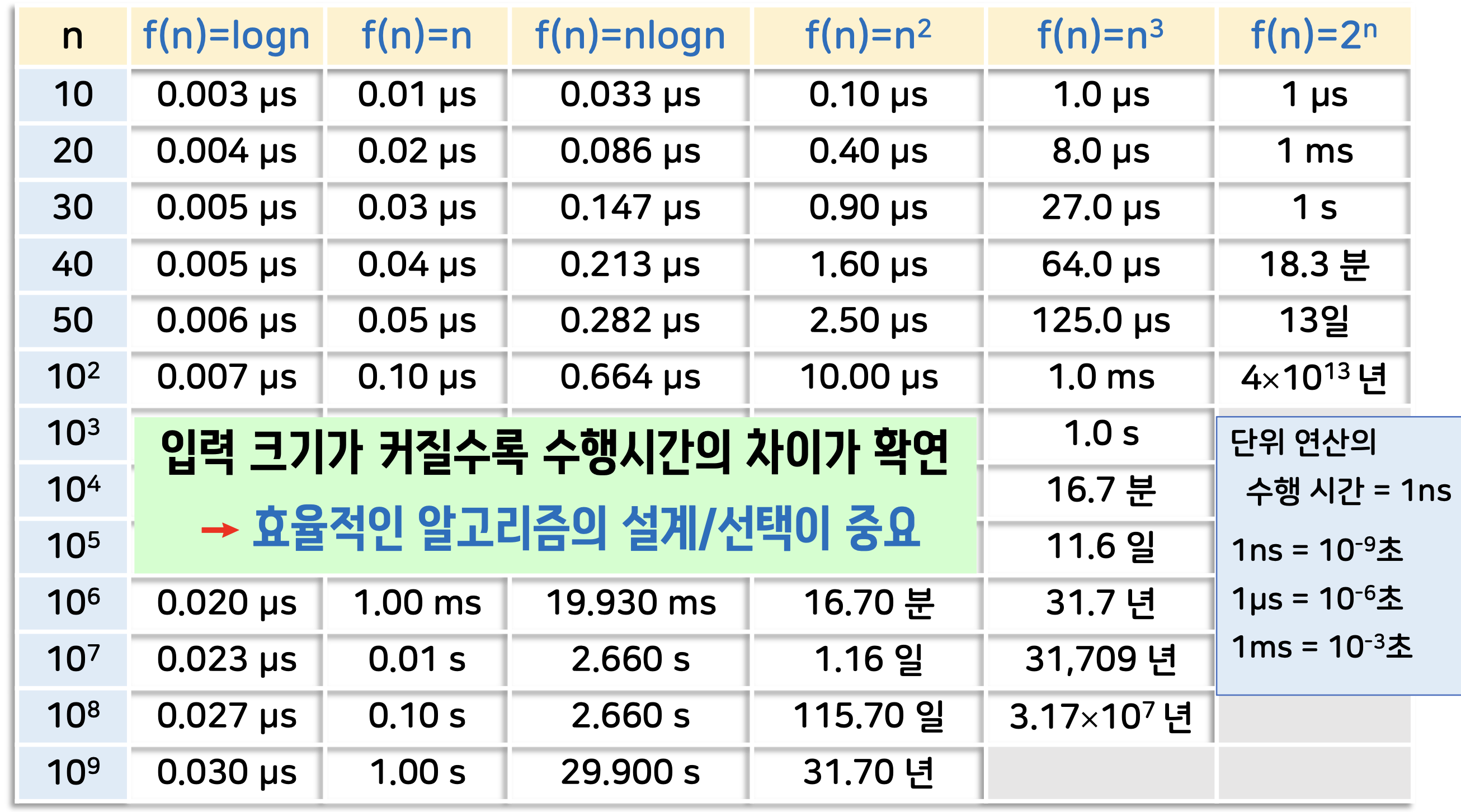
만약 나의 컴퓨터가 하나의 연산을 처리하는 시간이 1ns야,
그런데 10억개 10⁹가 들어왔을 때, f(n) = n²의 경우는 31.7년을 기다려야 한다!!
결국, 입력의 크기가 작을 때는 어떤 알고리즘을 쓰더라도 차이가 크게 나지 않을 수 있다.
하지만 입력 크기가 점점 커짐에 따라서 알고리즘 성능이 엄청 차이가남.
그래서 우리가 효율적인 알고리즘을 설계하고 사용하는 것을 중요하게 생각한다.
정리하기
1.알고리즘 분석
• 정확성 분석 + 효율성 분석
• 효율성 분석 → 공간 복잡도, 시간 복잡도(각 문장의 수행횟수의 합)
• 시간 복잡도 → 입력 크기의 함수와 최악의 수행시간으로 표현
2. 점근성능
• 입력 크기가 무한히 커짐에 따라 결정되는 성능 → 최고차수만으로 간략히 표현
• 표기법 → O-표기, Ω-표기, Θ-표기
• O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n)
3. 순환 알고리즘
• 순환 알고리즘의 수행시간은 점화식 형태로 정의되며, 폐쇄형을 구해서 표현
• 분할정복 방법이 적용된 알고리즘은 기본적으로 순환 알고리즘 형태를 가짐
• 기본 점화식과 폐쇄형
- 1. 알고리즘 분석
⦁ 알고리즘 분석 → 정확성 분석, 효율성 분석
⦁ 정확성 분석 → 올바른 입력이 주어졌을 때 유한 시간 내에 정확한 결과를 생성하는 지를 수학적으로 증명하는 것
⦁ 효율성 분석 → 알고리즘 수행에 필요한 컴퓨터 자원의 양을 측정
- 공간 복잡도 → 알고리즘 수행에 필요한 총 메모리의 양
- 시간 복잡도 → 알고리즘의 수행시간
⦁ 알고리즘 수행시간 → 알고리즘의 각 단위 연산(문장)이 수행되는 횟수의 합
- 입력 크기의 함수로 표현
- 데이터의 입력 상태에 따라 달라짐 → 최악의 수행시간으로 표현 - 2. 점근성능
⦁ 입력 크기가 무한히 커짐에 따라 결정되는 성능
- 수행시간의 다항식 함수에서 최고차항만을 계수 없이 취해서 단순하게 표현하는 방법 → 알고리즘 수행시간의 증가 추세를 나타내므로 알고리즘 간의 우열 표현/비교에 용이
- 요소 → 시작
⦁ 표기법
- O-표기(“Big-oh”) → 점근적 상한 → 알고리즘의 최악의 수행시간에 해당
- Ω-표기(“Big-omega”) → 점근적 하한 → 최선의 수행시간에 해당
- Θ-표기(“Big-theta”) → 점근적 상한과 하한을 동시에 표시
⦁ O–표기의 함수 간의 크기 관계 → O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n)
⦁ 실용적인 계산 방법 → 알고리즘에 나타난 루프(반복문)의 반복횟수를 조사하여 최고 차수를 시간 복잡도로 취함 - 3. 순환 알고리즘
⦁ 알고리즘의 수행 과정에서 자기 자신의 알고리즘을 다시 호출하여 수행하는 형태의 알고리즘
- 수행시간은 점화식으로 표현되고, 이를 풀어서 폐쇄형으로 표시
- 분할정복 방법의 적용된 알고리즘(이진 탐색, 퀵 정렬, 합병 정렬)은 기본적으로 순환 알고리즘 형태로 표현됨
⦁ 기본적인 점화식과 폐쇄형
① T(n) = T(n-1) + Θ(1), T(1)=Θ(1) → T(n) = Θ(n)
② T(n) = T(n-1) + Θ(n), T(1)=Θ(1) → T(n) = Θ(n2) → 퀵 정렬의 최악 수행 시간
③ T(n) = T(n/2) + Θ(1), T(1)=Θ(1) → T(n) = Θ(logn) → 이진 탐색의 수행 시간
④ T(n) = T(n/2) + Θ(n), T(1)=Θ(1) → T(n) = Θ(n)
⑤ T(n) = 2T(n/2) + Θ(1), T(1)=Θ(1) → T(n) = Θ(n)
⑥ T(n) = 2T(n/2) + Θ(n), T(1)=Θ(1) → T(n) = Θ(nlogn) → 퀵 정렬의 최선 수행 시간, 합병 정렬의 수행 시간
아 분량왜케 많아,
'방송통신대 컴퓨터과학과(25-02~ > 2025학년도 1학기' 카테고리의 다른 글
| 방통대 경영학원론 1강 요약 - 경영이란 (6) | 2025.02.27 |
|---|---|
| 방통대 알고리즘 3강 정렬 (1) - 기본개념, 선택, 버블, 삽입, 셀 (3) | 2025.02.27 |
| 방통대 알고리즘 1강 알고리즘 소개 (1) - 개념, 설계, 분석, 욕심쟁이, 분할정복, 동적 프로그래밍 (1) | 2025.02.19 |
| 방통대 원격대학교육의이해 (학습,내용,정답) (1) | 2025.02.18 |
| 25년 1학기 방통대 컴퓨터과학과 일정 (6) | 2025.02.17 |



