퀵이 내용 많아서 분리..
합병정렬?
주어진 배열을 동일한 크기의 두 부분배열로 분할하고,
각 부분배열에 순환적으로 합병 정렬을 적용하여 정렬시킨 후,
정렬된 두 부분배열을 합병하여 하나의 정렬된 배열을 만듦.
60 20 70 10 80 30 50 40
60 20 70 10 80 30 50 40 ==> 1.동일한 크기의 두 부분배열로 분할
합병정렬 합병정렬 ==> 2.합병정렬의 순환 적용(1 > 2 > 3)
10 20 60 70 30 40 50 80
10 20 30 40 50 60 70 80 ==> 3. 정렬된 두 부분배열의 합병
1,2,3 반복적으로 수행
합병정렬 알고리즘

부분배열인 B,C 비교, Merge로 합병.
얘도 봤더니 순환 알고리즘. 그래서 결론적으로는 합병정렬도 분할정복 방법이 적용된 방법이다.
합병정의 전체적인 수행과정
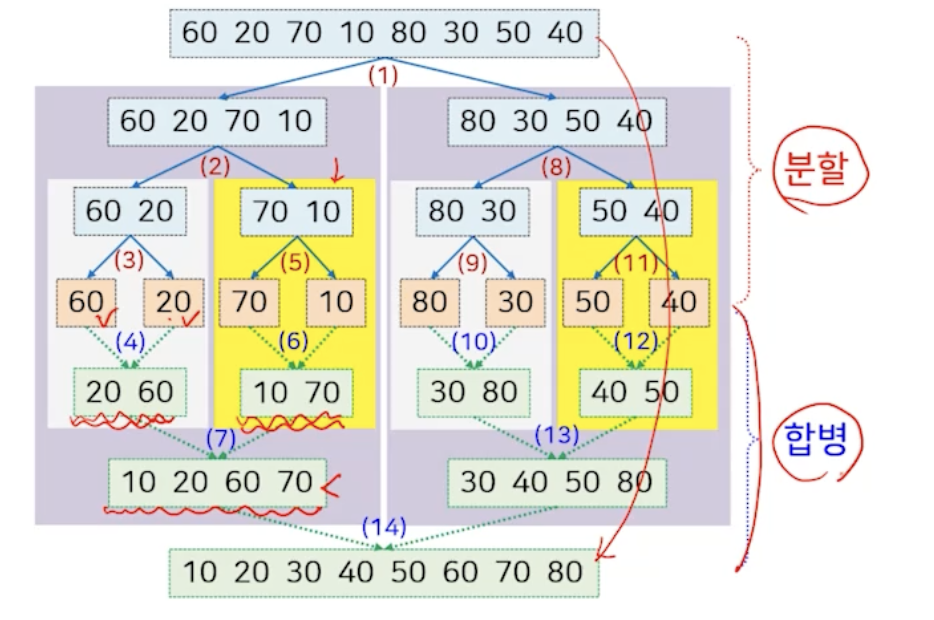
왼쪽 절반에 대한 결과 + 오른쪽 절반에 대한 결과 = 정렬된 두 부분배열의 결과를 합쳐서 정렬하면 됨.
합병 함수 Merge()

핵심은 두개의 정렬된 부분배열을 합치는 것.
B와 C는 각각 정렬된 결과가 있고 이것을 합치면됨.
if B와 C를 비교해서 자작은 데이터를 A[k]에 복사.
else 정렬된 부분 배열 B또는 C에 남아 있는 모든 데이터를 A로 복사
합병 함수 Merge()의 동작
n/2 = 4
n = 8
B[ ] 10 20 60 70 C[ ] 30 40 50 80 1.분할
B[n/2] 10 20 60 70 2.합병정렬
C[n/2] 30 40 50 80
B의 10과 C의 30을 비교 => A[n]에 10 넣음
B의 20과 C의 30을 비교 => A[n]에 20 넣음
B의 60과 C의 30을 비교 => A[n]에 30 넣음
B의 60과 C의 40을 비교 => A[n]에 40 넣음 ... ing
(마지막 한쪽에 수가 없어졌을때 나머지 숫자(80)을 넣음.)
==> A[n] 10 20 30 40 50 60 70 80 3.머지
성능과 특징
합병 함수의 Merge()수행시간
몇 번 비교하는 지 => 성능
B[n/2] C[n/2]
=> A[n]
두 부분배열 B와 C간의 비교 횟수

첫번째의 경우 4번의 비교
두번째의 경우 7번의 비교
최소는 n/2 이거나 많아야 n-1
==> 최악의 경우 ϴ(n)
= 퀵정렬의 분할함수와 동일한 최악의 경우 시간.
합병 정렬 MergeSort()의 수행시간

합병정렬 수행시간은 T(n)은 왼쪽 절반 + 오른쪽 절반 + 합병함수
T(n) = T(n/2) + T(n/2) + ϴ(n) (n>1), T(1) = 0
T(n) = 2T(n/2) + ϴ(n)
최선, 최악, 평균 수행시간은 T(n) = O(nlogn)
합병정렬은 안정적인 정렬 알고리즘이다.
: 합병 과정에서 동일한 두 데이터에 대해서 항상 왼쪽 데이터를 먼저 선택함
합병정렬은 제자리 정렬 알고리즘이 아니다.
: A[n] = B[n/2] + C[n/2] -> 입력 크기 n만큼의 추가적인 공간을 요구
A의 n갯수에 따라 B와 C의 크기가 늘어남
합병정렬은 전형적인 분할정복 방법이 적용 되어있다.
- 분할
주어진 배열을 동일한 크기의 2개의 부분배열로 분할
- 정복
각 부분배열에 대해서 합병 정렬을 순환적으로 적용하여 정렬함
- 결합
정렬된 두 부분배열을 합병하여 하나의 정렬된 배열을 만듦
비순환적 방식의 합병 정렬
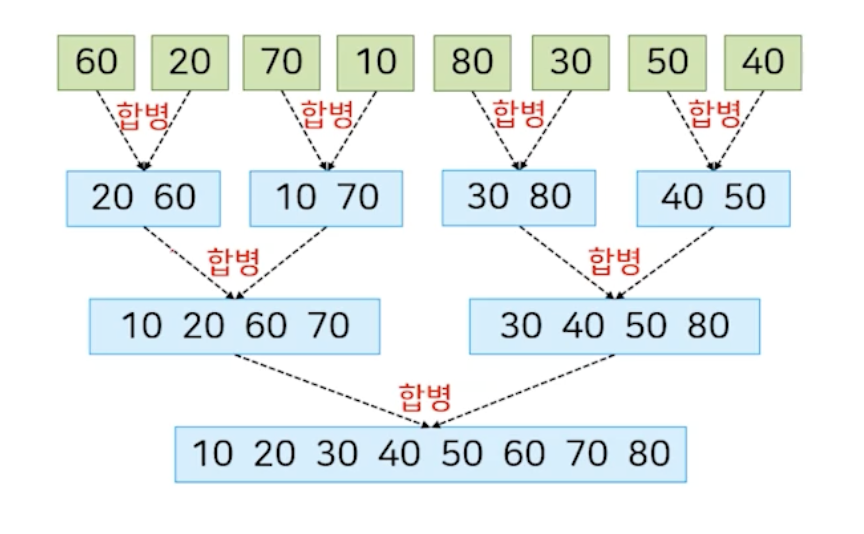
순환이 아니라 반복문을 가지고도 합병정렬 알고리즘을 표현할 수 있다. 순환사용 X의 경우
[정리하기]
1. 퀵 정렬
- "피벗", 분할함수O(n)
- 분할되는 두 부분배열의 크기에 따라 성능이 달라짐 -> 최악 O(n²), 최선/평균 O(nlogm)
- 불안정적, 제자리
- 피벗 선택의 임의성만 보장되면 평균적인 성능 O(nlogn)을 보임
- 분할정복 방법이 적용됨
2. 합병정렬
- 합병 함수 O(n), 최악/최선/평균 O(nlogn)
- 안정적 정렬, 제자리 정렬이 아님
- 전형적인 분할정복 방법이 적용됨
'방송통신대 컴퓨터과학과(25-02~ > 2025학년도 1학기' 카테고리의 다른 글
| 방통대 이산수학 1강 - 이산수학의 개요 (4) | 2025.03.12 |
|---|---|
| 방통대 경영학원론 2강 요약 - 경영의 역사 (6) | 2025.03.11 |
| 방통대 알고리즘 4강 정렬 (2) - 퀵 정렬 (5) | 2025.03.10 |
| 방통대 경영학원론 1강 요약 - 경영이란 (6) | 2025.02.27 |
| 방통대 알고리즘 3강 정렬 (1) - 기본개념, 선택, 버블, 삽입, 셀 (3) | 2025.02.27 |



