[학습개요]
명제와 명제가 아닌 것을 구분할 수 있어야한다.
다양한 논리연산의 기능을 이해하고 합성명제의 진리값을 구할 수 있어야한다.
한정자가 포함된 술어논리를 구사할 수 있다.
두 명제의 논리적 동치 여부를 판별할 수 있다.
추론규칙을 이용하여 타당한 추론을 판별한다.
2.1 명제란? proposition
참과 거짓을 구별할 수 있는 문장이나 수학적 식을 명제라고 함.
- 명제의 진리값 : 참(t) 거짓(f)
명제의 종류
- 합성명제
- 조건명제, 쌍조건 명제
- 항진 명제, 모순명제
명제의 예
명제인지 아닌지 구분하시오.
1) 6은 2의 배수다 o
2) 청수는 공부를 잘한다 x
3) x + 2 = 0
----
1) 참
2) 명제가 아님
3) x의 값에 따라서 참일 수도 있고, 거짓일 수도 있다. 따라서 명제가 아니다. ("명제함수", 정의 2.9에서 다시 다룸)
진리값을 구해라.
1) 2,3,6은 소수다. = F
2) 소수의 개수는 무한하다 = T (정리 13.9에서 다시 달루것)
3) 126 = 2⁶ = F
4) 지구에서 가장 높은 산은 에베레스트이다. = T
2.2 논리 연산
2.2.1 논리 연산자
2.2.2 조건명제
2.2.3 동치
실수집합
:0.5, 루트2 (실수는 변수,상수)
실수연산
:+ - x 나누기,
수식
:실수 연산식
논리집합에선 어떨까?
논리집합
논리 변수(아직 t인지 f인지 모르는 상태), 논리 상수(t,f)
t = 0
f = 0
논리연산
∨, ∧, ~ , ⊕
합성명제
: 논리 연산식
2.2.1 논리연산자
합성명제 (compound proposition)
:하나 이상의 명제와 논리연산자들이 결합되어 만들어진 명제를 합성명제라고 한다.
논리연산 종류
| 논리합 (OR, ∨) | p∨q | 둘 중 하나라도 참이면 참 | p = T, q = F → T |
| 논리곱 (AND, ∧) | p∧q | 둘 다 참일 때만 참 | p = T, q = T → T |
| 부정 (NOT, ¬) | ¬p | 참이면 거짓, 거짓이면 참 | p = T → F, p = F → T |
| 배타적 논리합 (XOR, ⊕) | p⊕q | 서로 다를 때 참 | p ≠ q → T |
- 논리합(∨) → 하나라도 참이면 참
- 논리곱(∧) → 둘 다 참일 때만 참
- 부정(¬) → 반대값으로 변경
- 배타적 논리합(⊕) → 서로 다를 때만 참
진리표 구하는 법 알아야함!!
2.2.2 조건명제
조건명제 (comditional proposition, →)
:명제 p와 q가 있을 때, 명제 p가 조건의 역할을 수행하고 명제 q가 결론의 역할을 수행하는 경우
p -> q (p=>q)
p는 q의 충분조건 : p가 일어나면 q가 일어나는 것을 보장
q는 p의 필요조건 : q가 일어나는데 p가 필요함.
p가 참이면 q도 반드시 참이어야 함
| p | q | p → q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
- 참 → 참 → 참
- 참 → 거짓 → 거짓 ❌ (조건이 성립하지 않음)
- 거짓 → 참 → 참 (p가 거짓이면 조건은 항상 참)
- 거짓 → 거짓 → 참 (p가 거짓이면 q의 값과 관계없이 참)
p가 참이면 뒤에 붙는 q에따라 T,F인지 판가름
p가 거짓이면 뒤에 상관없이 다 T참
쌍조건면제(biconditional proposition, )
:명제 p와 q가 있을 때, 명제 p와 q가 조건의 역할과 결론의 역할을 동시에 수행하는 경우
| p | q | |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
쌍조건명제는 두 명제가 같은 값을 가질 때만 참이 된다! 논리적으로 p와 q가 동치(Equivalent)일 때 참이 되는 논리연산이다.
- p와 q가 둘 다 참 → 참
- p와 q가 둘 다 거짓 → 참
- p와 q가 다르면 → 거짓
나는 학생일 때만 학생증을 가지고 있다.
- p: "나는 학생이다."
- : "나는 학생증을 가지고 있다."
- 학생이면 학생증을 가지고 있고, 학생이 아니면 학생증이 없다.
- 따라서 두 조건이 같을 때만 참이므로 쌍조건명제가 된다.
2.2.3 동치
논리적 동치 (lgocal equivalence, ≡)
:두 명제 p와 q가 논리적으로 동등하면 논리적 동치라고 하고 , p ≡ q로 표시한다.
논리적으로 동등하다는 말은 두 명제가 항상 동일한 진리값을 가진다는 의미!
이 명제와 이 명제가 동치임을 증명하세요, 하면 진리표를 작성해서 둘이 같은가를 보면 됨.
- p
- 역, 이, 대우
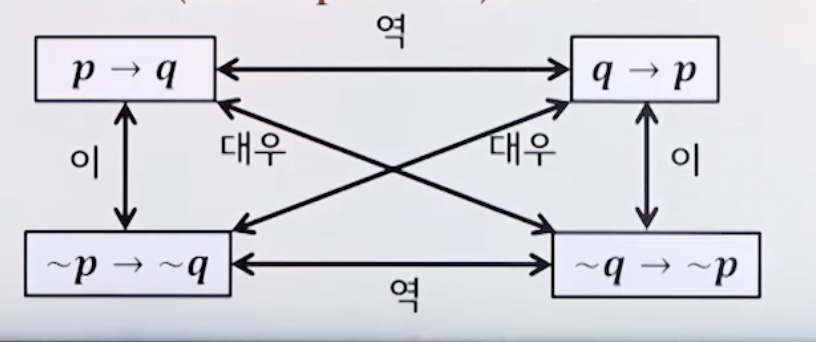
조건명제 p → q (q이면 p이다)
- 역(converse) : q → p , q면 p이다.
- 이(inverse) : ~p → ~q, 낫p이면 낫q이다
- 대우(contrapositive) : ~q → ~p, 낫q이면 낫p이다. (거꾸로 놓되 낫을 붙인다.)
"비가 오지 않거나, 땅이 젖었다"는 "비가 오면 땅이 젖는다"와 동치인가?
- : "비가 온다"
- : "땅이 젖는다"
- 주어진 문장: ¬P∨Q
- 조건명제: P→Q ≡ ¬P∨Q
- 두 명제가 동일하므로 논리적 동치! ✅
논리적 동치법칙
(47:00)
(1)교환법칙 (commutation law)
(2)결합법칙 (associative law)
(3)분배법칙 (distributive law)
(4)항등법칙(indentity law) : p가 T아니면 F만 생각.
p∨F ≡ p
p∧T ≡ p
(5)지배법칙 (domination law) : 이미 F,T면 p에 관계없이
p∨T ≡ T
p∧F ≡ F
(6)부정법칙 (negation law) :
~T ≡ F
~F ≡ T
p∨(~p) ≡ T
p∧(~p) ≡ F
(7)이중 부정 법칙(domination negation law) : 거짓의 거짓이면 긍정이다. 원래 명제의 반대에서 반대를 하면 원래 명제와 같다.
~(~p) ≡ p
(8) 멱등법칩(idempotent law): p가 몇개로든 연결되면 p다
p∨p ≡ p
p∧p ≡ p
(9) 드 모르간 법칙(de Morgan's law): 집합에서 등장, p와 q의 or 낫은 , 합이었으면 or로 바뀌는
~(p∨q) ≡ (~p) ∧ (~q)
~(p∧q) ≡ (~p) ∨ (~q)
(10) 흡수법칙 (absorption law)
p∨(p ∧ q ) ≡ p
p∧(p ∨ q ) ≡ p
(11) 합축법칙(implication law) : 간혹 시험에 출제, p이면 p이다, 조건명제에서 달리표현하면 이렇게도 표현한다는 뜻.
p → q ≡ ~p∨q
(12) 대우법칙 : 이것도, 낫q이면 낫p이다
p → q ≡ ~q → ~p
드 모르간 법칙을 사용해서 다음식의 부정을 나타내라
문제 ) -2 < x <3

ㅎ..
시험은 다음 명제중, 항진명제(tautology)를 골라라, 모순명제(contradiction)를 골라라 이런식으로 출제됨.
항상 참인 = 항진명제 p∨T
항상 거짓 = 모순명제 p∧F
2.3 술어논리
'방송통신대 컴퓨터과학과(25-02~ > 2025학년도 1학기' 카테고리의 다른 글
| 방통대 이산수학 1강 - 이산수학의 개요 (4) | 2025.03.12 |
|---|---|
| 방통대 경영학원론 2강 요약 - 경영의 역사 (6) | 2025.03.11 |
| 방통대 알고리즘 4강 정렬 (2) - 합병 정렬 (1) | 2025.03.11 |
| 방통대 알고리즘 4강 정렬 (2) - 퀵 정렬 (5) | 2025.03.10 |
| 방통대 경영학원론 1강 요약 - 경영이란 (6) | 2025.02.27 |



